Morphing Planar Graphs in Spherical Space

Stephen G. Kobourov and Matthew Landis

Abstract

We consider the problem of intersection-planar graph morphing, and in particular, a generalization from Euclidian space to spherical space. We show that under certain conditions, there exists a continuous and intersection-free morph between two sphere drawings of a maximally planar graph, where sphere drawings are the spherical equivalent of plane drawings: crossings-free geodesic-arc drawings. In addition to the existence proof, we describe a morphing algorithm along with its implementation.

Summary of Algorithm

We begin with source and target drawings of the same graph on a sphere, such as these:

Source (S)	Target (T)

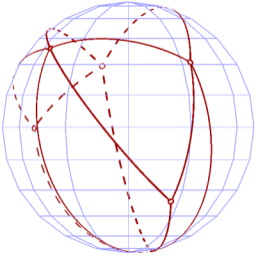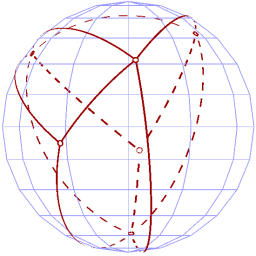We then "slide" both source and target down to the lower hemisphere, resulting in the following:

S'	T'

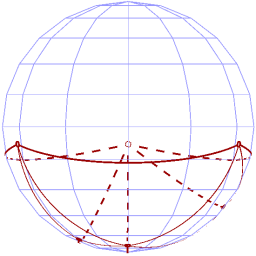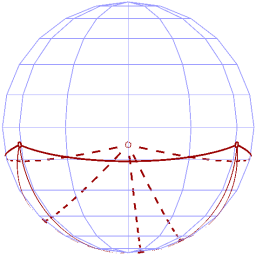Now that both our drawings occupy only the lower hemisphere, we can apply the Gnomonic Projection to each, to get two crossing-free plane drawings of the graph, as shown:

S''	T''

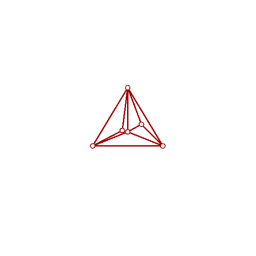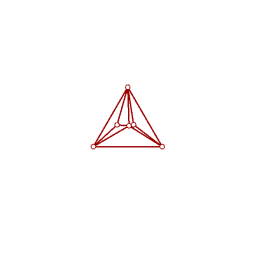We then use an existing plane morphing algorithm to get from one planar drawing to the other, while performing the inverse gnomonic projection of the intermediary steps back up onto the sphere throughout, and we have a full morph from S to T that does not introduce crossings.

Animations

smorph1.avi (11 MB)

smorph2.avi (11 MB)

The six panes displayed in the movies are:

Source sphere drawing (S)	Current sphere drawing (where the morph takes place)	Target sphere drawing (T)
Source plane drawing (S'', the gnomonic projection of S')	Current plane drawing (during plane stage of morph, S'' -> T'')	Target plane drawing (T'', the gnomonic projection of T')